How do you find the rate of change?

The rate of change refers to how much something for example distance is changing in a specific unit of time. In order to work out the rate of change, you must divide the thing that is changing with how much it has changed in such a unit of time.

Derivatives are the best tool, but not for everyone... Considering two variables (distance and time, for example), you can also take the first and last value of both in a certain process, subtract the ones from the same variable (e.g. last and first distances of the bus from your position) and divide the subtractions of different variables. By doing this with position/distance and time, the rate of change you get is the speed of the object you're analyzing!

The rate of change tells us how quickly something changes over time, like how fast a car is going or how tall a plant grows. To find it, you look at two points: where you started and where you ended up. You then measure the change in distance and the change in time. For example, if a car travels 120 miles in 2 hours, you can find its speed by dividing the distance (120 miles) by the time (2 hours), which gives you a rate of change of 60 miles per hour.

The rate of change measures how one quantity changes relative to another. In mathematics, it is often calculated using derivatives in calculus or the difference between two points in algebra. Here are the common methods to find the rate of change:

1. Average Rate of Change (Algebraic Approach)

The average rate of change between two points on a function is calculated as the slope of the line connecting the points. This is given by:

2. Instantaneous Rate of Change (Using Derivatives)

The instantaneous rate of change of a function at a specific point is the value of the derivative at that point.

This gives the slope of the tangent line to the curve at x=ax = ax=a, representing how the function changes at that exact point.

The average rate of change represents the average rate at which something changes from one point to another.

So you need to set up the equation like this:

Rate of change of {x} = (change in x) divided by time taken for the change to happen.

E.g. Rate of change of distance is acceleration.

a = d2 - d1 / t

Distance traveled divided by time it takes. On a graph that would be calculating the difference in the change in y and the change in x

The rate of change measures how a quantity changes over time or across space. It's often represented as the slope of a line connecting two points on a graph.

Divide the change of one variable with the change of the other variable

Linear functions have a constant rate of change which is represented as the gradient of the graph.

It is simply the change of y-values with respect to x-values i.e. (y1-y2) / (x1-x2) where (x1,y1), (x2,y2) are the coordinates

the change in y-values by the change in x-values.

To find the rate of change, you must divide the change in y by the change in x (if using a graph, where y is the vertical axis and x is the horizontal axis).

Hello Mrs Vickie Shanahan. There isn't much context to your question here, so I'll keep my response as general as possible:

The rate of change describes a relationship between a dependent and an independent variable. For example, the rate of change of velocity with time or the rate of change of temperature with distance.

In a simple mathematical case, we'd write this as the change in the dependent variable (temperature, dT) over a fixed interval of the independent variable (distance, dx)

Which is mathematically written as dT/dx, or as shown in the graph, dy/dx.

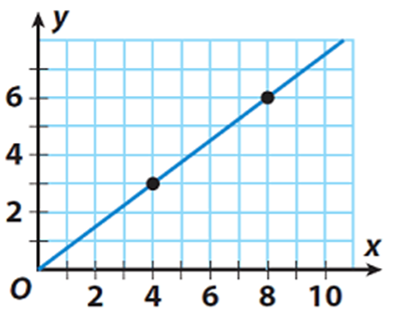
It is then clear that for the linear relationship in the above graph, the rate of change is dy/dx = (y1-y2)/(x2-x1) = (6-3)/(8-4).

There are a couple of ways to find this. If your data is displayed in graph format, you can find the rate of change by dividing the change in y-values by the change in x-values. If you are talking about the instantaneous rate of change (this is called the derivative of a function) then we need to look further at the function itself.

The rate of change tells us how one thing changes compared to another. For example, if you're looking at how far a car travels over time, the rate of change would be its speed—how many meters the car moves every second.

First we need to know how much each of these things changes. You do this by subtracting the starting value from the ending value. For example, if a car moves from 10 meters to 30 meters in 4 seconds, the change in distance is 20 meters, and the change in time is 4 seconds.

Then you divide the change in distance by the change in time to get the rate of change. In this case, the car is moving at 5 meters per second. This means every second, the car travels 5 meters.

Hope this helps :)