How do you find the rate of change?

Use the formula (new-old)/old and multiply by 100 to get a percentage

the change in y-values by the change in x-values.

The rate of change (ROC) is how much the value of something changes over a period of time and it is given in percentage terms.

To find this you first calculate the change in "Y" values (or the change in an outcome variable) divided by the change in "X" values (or the change in input variables).

So if my tutoring time increases from 3 hours in week 1 to 16 hours in week 2 and my income increases from £45 per week to £240 per week, Y values are my income and X values are the work hours I put in. r

To calculate the ROC I would do the following.

(240 - 45) / (16 - 3) = 195 / 13 = 15% rate of change in my earnings between week 1 and week 2.

If you take the change in Y values and divide that with the change in X-values the result will be a rate of change,

In a graph of a value vs time, it would be the gradient. Otherwise simply divide the difference in any particular value by the time taken.

The rate of change can be found by calculating the difference in the values of a quantity over a certain period of time or another variable. It is often calculated using the formula:

Rate of change = (Change in quantity) / (Change in time or another variable)

For example, to find the rate of change of distance with respect to time, you would divide the change in distance by the change in time. This gives you the speed or velocity.

The rate of change tells us how quickly something changes over time, like how fast a car is going or how tall a plant grows. To find it, you look at two points: where you started and where you ended up. You then measure the change in distance and the change in time. For example, if a car travels 120 miles in 2 hours, you can find its speed by dividing the distance (120 miles) by the time (2 hours), which gives you a rate of change of 60 miles per hour.

The rate of change measures how one quantity changes relative to another. In mathematics, it is often calculated using derivatives in calculus or the difference between two points in algebra. Here are the common methods to find the rate of change:

1. Average Rate of Change (Algebraic Approach)

The average rate of change between two points on a function is calculated as the slope of the line connecting the points. This is given by:

2. Instantaneous Rate of Change (Using Derivatives)

The instantaneous rate of change of a function at a specific point is the value of the derivative at that point.

This gives the slope of the tangent line to the curve at x=ax = ax=a, representing how the function changes at that exact point.

The rate of change measures how a quantity changes over time or across space. It's often represented as the slope of a line connecting two points on a graph.

Rate of change can be calculated by the amount of a specific quantity is changing by the time it took for the change to hapen. A common example in physics in speed which is simply rate of change of position(or distance). If a car changes its position by 20 miles in 30 minnutes then its average speed(or rate of change of position) is 20miles divided by 30min(or 0.5 hr) which is 40 miles per hr

Difference divided by the time.

In terms of a graph, this will be the change in the y-axis divided by the change in the x-axis (aka slope).

By finding the gradient of the line. You can do this by using the formula: m = (y2 — y1) / (x2 — x1). Where m is the gradient.

Divide the change of one variable with the change of the other variable

Hello Mrs Vickie Shanahan. There isn't much context to your question here, so I'll keep my response as general as possible:

The rate of change describes a relationship between a dependent and an independent variable. For example, the rate of change of velocity with time or the rate of change of temperature with distance.

In a simple mathematical case, we'd write this as the change in the dependent variable (temperature, dT) over a fixed interval of the independent variable (distance, dx)

Which is mathematically written as dT/dx, or as shown in the graph, dy/dx.

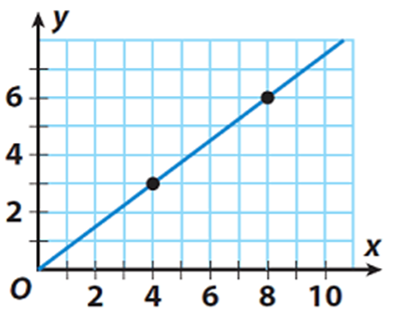
It is then clear that for the linear relationship in the above graph, the rate of change is dy/dx = (y1-y2)/(x2-x1) = (6-3)/(8-4).

Derivatives are the best tool, but not for everyone... Considering two variables (distance and time, for example), you can also take the first and last value of both in a certain process, subtract the ones from the same variable (e.g. last and first distances of the bus from your position) and divide the subtractions of different variables. By doing this with position/distance and time, the rate of change you get is the speed of the object you're analyzing!